The below table shows the probability of at least N new Bitcoin blocks in the next T minutes.
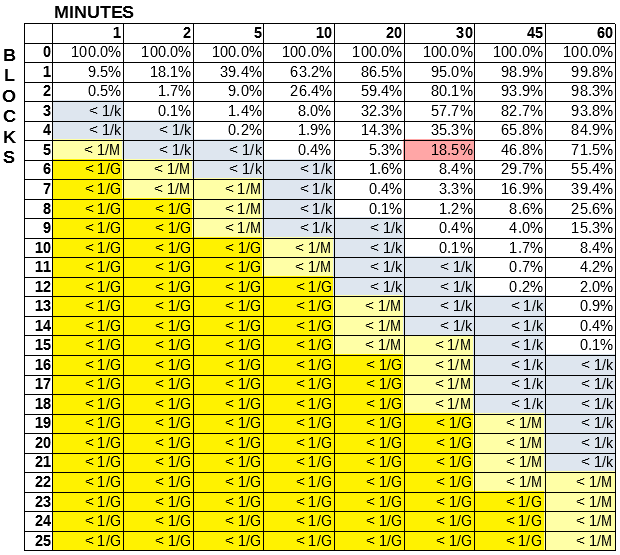
The red cell is just an example. It tells there’s an 18.5% chance of getting 5 or more new blocks within the next 30 minutes.
“< 1/k” means less than a one in thousand chance of occurring.
“< 1/M” means less than one in a million.
“< 1/G” means less than one in a billion.
How It Relates to Counterparty DEX
If I buy a token with BTC on the Counterparty DEX, I must send the Bitcoins before 20 blocks have passed. From this table I learned that this almost certainly equates to more than one hour. The light blue cell means a deadline shorter than one hour has a likelihood of less than one in a thousand. To be on the extreme safe side, I can say that 20 blocks never happen in less than 30 minutes. The likelihood of this is less than one in a billion.
Calculations
Every second the probability of one new block, p, is 1/600.
I ignored the tiny chance of two blocks at the same second. This is not just a convenient assumption, it’s actually realistic. Due to network latency, if two blocks are found too close together, one is orphaned.
One block is expected (E = 1) per 10 minutes (n = 600 seconds).
This is in accordance with the fundamental property (E = np) of independent binomial trials; 1 = 600 * 1/600.
Next I used the probability mass function
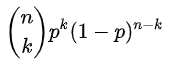
to determine the chance of finding exactly k blocks in n seconds.
This was done in Open Office Calc.
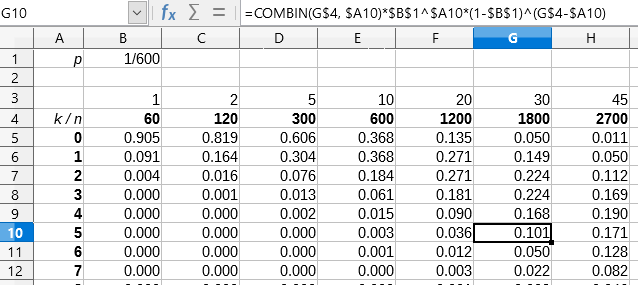
In the final table I simply added every cell below to the current cell. You can see here that the prob of getting exactly 5 blocks in 30 minutes is 10.1%. When you add the values of 6, 7, 8, etc blocks you get to 18.5% as in the first example.
Categories: Uncategorized